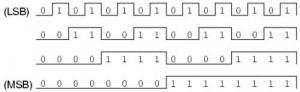
Последовательность счёта в двоичных счётчиках

Заметьте, как младший двоичный разряд меняется с нуля на единицу в каждом новом члене последовательности, тогда как каждый последующий разряд меняет свое состояние на противоположное с частотой, равной половине частоты смены состояния предыдущего разряда. Старший двоичный разряд меняется лишь один раз за всю последовательность из шестнадцати членов: на переходе от седьмого (0111) к восьмому члену (1000).
Если бы мы задались целью сконструировать схему четырёхразрядного двоичного счётчика, то всё что нам надо было бы сделать — создать последовательность частотных делителей, в которой каждая схема делила бы прямоугольный импульс на два:
Для решения этой задачи идеально подходят J-K-триггеры, так как они способны менять выходной сигнал на противоположный по синхроимпульсу, когда на оба входа J и K поданы сигналы высокого уровня (1):
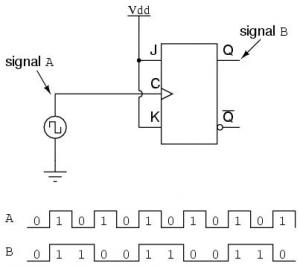
Приняв два сигнала (A и B) в этой схеме за два разряда двоичного числа, где сигнал A будет младшим двоичным разрядом, а сигнал B — старшим двоичным разрядом, мы увидим, что последовательность будет обратной: 11, 10, 01, 00 и снова 11. Возможно, схема считает и не в том направлении, в каком мы предполагали, но тем не менее считает!
РЕЗЮМЕ:
В двоичных счетных последовательностях существует закономерность деления частоты: частота перехода от 0 к 1 для каждого разряда, от младшего к старшему, уменьшается в два раза. Проще говоря, каждый последующий разряд будет переходить с 0 на 1 и обратно с частотой в два раза меньшей частоты смены предыдущего разряда.
Можно сконструировать схемы на J-K-триггерах в режиме переключения между двумя состояниями, которые будут «считать", используя двоичную систему счисления.